http://www.juegos.com/juego/math-apocalypse
miércoles, 14 de octubre de 2015
Juego de matemática #2
Esta vez traemos a su disposición otro juego flash de matemática, en el cual la dificultad va aumentando a medida que van pasando los niveles y resulta un reto aun más complicado para proteger nuestra base de los enemigos que se acercan, los cuales mediante soluciones vamos derrotando.
Juego de matemática
En esta ocasión les mostraremos un juego flash en el cual debes lograr que la suma de dos números de la misma que de los otros dos para que la balanza se mantenga estable.
http://www.juegos.com/juego/monkey-math-balance
Juego matemático japones
JUEGOS RELACIONADOS CON LA MATEMÁTICA
PROBLEMAS DE INGENIO CON GEOMETRÍA:
El templo japonés
Los juegos mentales están inspirados en el sangaku, la geometría del templo japonés que floreció en los siglos XVII, XVIII y XIX. En esos tiempos, sangaku (palabra japonesa para la tablilla matemática) era un pasatiempo nacional para todos, desde los campesinos hasta los nobles samurai. Resolvían los acertijos geométricos y luego ofrecían las soluciones a los espíritus, en forma de tablillas de madera elegantemente diseñadas y ejecutadas.
El templo japonés
Los juegos mentales están inspirados en el sangaku, la geometría del templo japonés que floreció en los siglos XVII, XVIII y XIX. En esos tiempos, sangaku (palabra japonesa para la tablilla matemática) era un pasatiempo nacional para todos, desde los campesinos hasta los nobles samurai. Resolvían los acertijos geométricos y luego ofrecían las soluciones a los espíritus, en forma de tablillas de madera elegantemente diseñadas y ejecutadas.
Esas tablillas, en las que estaban grabados los problemas geométricos, colgaban de los techos de templos y altares. En realidad, las mejores tablillas sangaku eran trabajos de arte que se realizaban en homenaje a los espíritus que habían ayudado a encontrar su solución. Actualmente son muy pocos los que recuerdan el sangaku.
En 1989, Hidetoshi Fukagawa y Daniel Pedoe publicaron la primera colección de sangaku traducida al inglés, libro que luego se publicitó en un artículo de Scientific American. Sin embargo, han sobrevivido más de 880 tablillas. Los problemas generalmente implicaban construcciones geométricas, muchas veces eran círculos dentro de círculos, triángulos o elipses. El nivel de dificultad iba de lo simple a lo imposible pero, según los patrones contemporáneos, todos serían considerados matemática recreativa. Algunos ejemplos siguen abajo:

Generalmente no se presentaba la resolución de los problemas o teoremas, sino sólo los resultados. Durante esa época, muchos japoneses amaron la matemática y disfrutaron de ella y se sintieron subyugados por la belleza de la geometría. Los autores del sangaku probablemente fueran maestros y sus alumnos. Las tablillas se realizaban con cuidado y la intención era que fueran ayudas visuales tanto para matemáticos como para legos.
Matemáticos griegos
REVOLUCIONARIOS DE GRECIA
LA CIENCIA EN ALEJANDRÍA
ALEJANDRÍA, CAPITAL DE LA CIENCIA
Alejandría fue la capital intelectual del mundo helenístico y el más importante centro de los descubrimientos científicos de la antigüedad. Ptolomeo (el sabio), el primero de los Lágidas, fundó el Museo (edificio consagrado a las musas), e inició la gran transformación de la ciudad en ese sentido.
ALEJANDRÍA, CAPITAL DE LA CIENCIA
Alejandría fue la capital intelectual del mundo helenístico y el más importante centro de los descubrimientos científicos de la antigüedad. Ptolomeo (el sabio), el primero de los Lágidas, fundó el Museo (edificio consagrado a las musas), e inició la gran transformación de la ciudad en ese sentido.
El museo comprendía el jardín botánico, el zoológico, un observatorio, habitaciones para sus miembros, gabinetes de trabajo, un gran comedor y sobre todo una incomparable biblioteca de cerca de 700 000 volúmenes. Los sabios, dedicados enteramente a sus investigaciones, y rodeados de condiciones excepcionales, realizaron notables trabajos. Todo manuscrito que llegaba a Alejandría se incorporaba inmediatamente a la biblioteca. Se hacía una copia que se entregaba a su dueño y el original quedaba en la biblioteca.
Numerosos eruditos se dedicaron a revisar los textos de las grandes obras. Fundaron la Filosofía, ciencia de las bellas letras. Aristarco preparó una edición de Hornero. Otros sabios se dedicaron a las matemáticas y a la astronomía. Euclides organizó las nociones de Geometría en una serie de teoremas rigurosamente encadenados.
Arquímedes, un siciliano que estudió ciencias en Alejandría, pero pasó su vida en Siracusa donde lo mató un soldado romano, calculó la superficie del cilindro y la esfera, y estableció el principio que lleva su nombre. Este extraordinario sabio, el más grande quizás de la antigüedad, fue también notable ingeniero que inventó aparatos de guerra, más tarde utilizados por los romanos.
Aristarco de Samos concibió la teoría de que el sol estaba fijo en el centro del universo, sin llegar a demostrarlo. Hiparco dio nombre a más de ochocientas estrellas y fijó su posición. Erastótenes de Cirene (Q I), llegó a calcular con una precisión asombrosa el largo del meridiano, con un error de apenas 400 Km. sobre un total de 40.000 Km.
Aristóteles no sólo fue un gran filósofo. Es notable su interés por las ciencias biológicas. Sus estudios sobre el mundo animal, en especial los insectos, revelan una seria curiosidad científica. En la isla Mitilene pasó dos años junto al mar, antes de enseñar a Alejandro, y allí adquirió numerosos y profundos conocimientos sobre ciencias naturales.
Son interesantes sus estudios sobre moluscos, cangrejos y langostas, sobre los peces (hábitos y migraciones) y sobre la abeja] en el que analiza las varias calidades de la miel, según las flores de donde se extrae el néctar. Así, pues, con sabios como Euclides, Arquímedes y Aristóteles, las ciencias, separadas de In filosofía, adquirieron un inusitado esplendor. Estos conocimientos teóricos, sin embargo no tuvieron aplicación practica.
No sintieron la necesidad de aprovecharlos, porque la esclavitud les solucionaba muchos problemas. En la técnica los griegos se mostraron poco creadores.
La civilización griega alcanza un nuevo brillo en el período helenístico. En Oriente, las clases dirigentes sometidas políticamente a los griegos se helenizan. Roma, conquistadora de monarquías helenísticas, adopta su civilización y la lleva a Occidente.
En este vasto imperio, desde la India a Gibraltar, la acción helenística se ejercerá en forma desigual. Será superficial en Oriente, donde las masas populares se mantienen fieles a sus viejas civilizaciones; en Occidente será en cambio, más profunda y duradera. Al seguir el curso de la historia vemos que la herencia de Grecia se ha convertido, a través de numerosos “renacimientos”, en parte integrante de nuestra civilización.
Conjetura de Goldbach
CONJETURA DE GOLDBACH
Hace muchos años se investiga un problema que hasta día de hoy resulta imposible de resolver, la conjetura de Goldbach. Este tema ha logrado inspirar tanto a ciertas personas que pasaron años de su vida intentando encontrar la respuesta y hasta algunas hicieron películas como "La habitación de Fermat". Aquí dejamos el adelanto de la película mencionada
https://www.youtube.com/watch?v=5O4RpFjipCI
domingo, 2 de agosto de 2015
21 Blackjack
Un grupo de estudiantes avanzados y un profesor de matemáticas diseñan un sistema para ganar al blackjack en Las Vegas. Por supuesto que todo el proceso está basado en problemas matemáticos complicados con los cuales consiguen su objetivo: pagar la universidad.
Aquí el trailer:
Aquí el trailer:
Si te gustó el trailer aquí la película completa:
Sucesión de Fibonacci
La sucesión de Fibonacci
La sucesión de Fibonacci es la sucesión de números:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Cada número se calcula sumando los dos anteriores a él.
- El 2 se calcula sumando (1+1)
- Análogamente, el 3 es sólo (1+2),
- Y el 5 es (2+3),
- ¡y sigue!
Ejemplo: el siguiente número en la sucesión de arriba sería (21+34) = 55
¡Así de simple!
Aquí tienes una lista más larga:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...
Y aquí un vídeo explicativo con muchas casualidades en la vida cotidiana de la sucesión de Fibonacci.
Ángulos
Ángulos cóncavos y convexos: clasificación
Los ángulos se clasifican según su amplitud:
Convexos: 0° = Nulo
Entre 0° y 90°= Agudo
90° =Recto
Entre 90° y 180° = Obtuso
180° =Llano
360°= 1 giro
Cóncavos: entre 180° y 360°
+El plano queda dividido en dos ángulos; uno cóncavo y otro convexo.
+Un ángulo es cóncavo cuando mide entre 180 y 360 grados. Si no es convexo.
Ángulos complementarios y suplementarios
Los ángulos se clasifican según su amplitud:
Convexos: 0° = Nulo
Entre 0° y 90°= Agudo
90° =Recto
Entre 90° y 180° = Obtuso
180° =Llano
360°= 1 giro
Cóncavos: entre 180° y 360°
+El plano queda dividido en dos ángulos; uno cóncavo y otro convexo.
+Un ángulo es cóncavo cuando mide entre 180 y 360 grados. Si no es convexo.
Ángulos complementarios y suplementarios
- Dos ángulos son complementarios cuando la suma de sus amplitudes es igual a 90°.
- Dos ángulos son suplementarios cuando la suma de sus amplitudes es igual a 180°.
domingo, 12 de julio de 2015
Canción de los números
Esta es una canción infantil que te enseña los números de una forma divertida. Lo hace con formas y personas que vemos cotidianamente.
Números racionales
Un número es racional (Q) cuando puede ser expresado como un cociente entre dos números enteros.
Los números racionales se expresan mediante una fracción o una expresión decimal.
En una fracción, el denominador indica el número de partes iguales en que se divide el entero; y el numerador, cuántas de esas partes se deben considerar.
Para encontrar la expresión decimal de una fracción se halla el cociente entre el numerador y el denominador.
Las expresiones decimales pueden ser finitas o periódicas.
- 3/4= 3:4= 0.75 FINITA
- 2/3=2:3= 0.6666... PERIÓDICA PURA
- 7/30=7:30= 0.2333333... PERIÓDICA MIXTA
Cuerpos geométricos
Los poliedros son cuerpos cuyas caras son polígonos. Se clasifican en prismas y pirámides.



Prisma triangular Prisma cuadrangular Prisma rectangular


Prisma pentagonal Prisma hexagonal
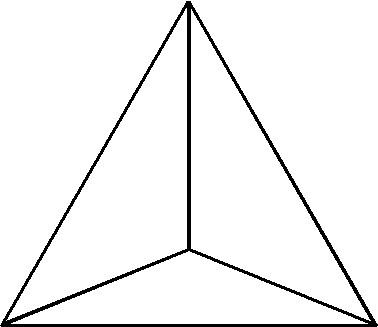


Pirámide triangular Pirámide cuadrangular Pirámide pentagonal

Pirámide hexagonal



Cono Cilindro Esfera
- Un prisma regular tiene dos polígonos paralelos e iguales como bases y las caras laterales son rectángulos iguales. Cuando las caras laterales son perpendiculares a las bases, los prismas son rectos.



Prisma triangular Prisma cuadrangular Prisma rectangular


Prisma pentagonal Prisma hexagonal
- Una pirámide regular tiene un polígono regular como base y las caras laterales son triángulos isósceles iguales. Todas las caras laterales concurren en un punto llamado cúspide.



Pirámide triangular Pirámide cuadrangular Pirámide pentagonal

Pirámide hexagonal
- Los cuerpos redondos son aquellos que tienen, por lo menos, una cara no plana y pueden rodar en alguna posición.



Cono Cilindro Esfera
sábado, 20 de junio de 2015
Teorema de pitágoras
Teorema de Pitágoras
Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos:
... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos! |
El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)
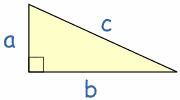
Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²):
a2 + b2 = c2
|
sábado, 13 de junio de 2015
Números enteros
NÚMEROS ENTEROS
Los números naturales (N) se utilizan básicamente para contar y para expresar cantidades enteras. Pero no son suficientes para expresar, por ejemplo, deudas o temperaturas bajo cero, por eso, es necesario recurrir a los números negativos.
Los números naturales, el cero y los números negativos forman el conjunto de los números enteros o números Z.
Z= ...-4;-3;-2;-1;0;1;2;3;4...
El 0 no es positivo ni negativo y tampoco es par o impar.
ADICIÓN Y SUSTRACCIÓN DE NÚMEROS ENTEROS
Para sumar y restar números enteros, se realizan los siguientes procedimientos:
+7+7=+18 Si ambos son positivos, se suman; y la suma es positiva
+5-12=-7 } Si tienen distinto signo, al de mayor modulo, se le resta el de menor módulo; y el -8+13=5 } resultado lleva el signo del mayor de los números.
-2-6=-8 Si ambos son negativos, se suman los módulos; y la suma es negativa
SUPRESIÓN DE PARÉNTESIS
Para suprimir un paréntesis, se debe tener en cuenta el signo que lo antecede:
- Si es un +, los signos que están dentro del paréntesis NO cambian
- Si es un -, los signos que están dentro del paréntesis CAMBIAN.
MULTIPLICACIÓN Y DIVISIÓN
Para multiplicar o dividir dos números enteros, se aplica la regla de los signos:
|
Signo de un factor
|
Signo del otro factor
|
Signo del producto o cociente
|
|
+
|
+
|
+
|
|
+
|
-
|
-
|
|
-
|
+
|
-
|
|
-
|
-
|
+
|
martes, 9 de junio de 2015
Truco matemático
En el día de hoy voy a hacer un truco de magia matemático. Y es este:
Piensa tu edad...
Ahora, restale 4...
Ahora, sumale 10...
Ahora, restale tu edad...
Es obvio que te dio 6.
Puedo asegurar que te quedaste impactado.
Piensa tu edad...
Ahora, restale 4...
Ahora, sumale 10...
Ahora, restale tu edad...
Es obvio que te dio 6.
Puedo asegurar que te quedaste impactado.
domingo, 31 de mayo de 2015
Números primos
¿Qué son y cuáles son los números primos?
Los números primos son todos aquellos números que únicamente pueden dividirse por el 1 y por ellos mismos para que de un número entero. Por ejemplo: el número 3 es un número primo porque solamente puede dividirse por él mismo o por el 1 para que de un número entero, si hacemos 3:2, el resultado es 1,5. En cambio si hacemos 3:1 o 3:3 el resultado será un número entero.
DATO INTERESANTE: El único número primo, que es par y se encuentra debajo del 100 es el número 2.
A continuación podremos observar todos los números primos que se encuentran debajo del 100:
2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59;61;67;71;73;79;83;89;97.
viernes, 22 de mayo de 2015
Ecuaciones
Esto es una breve explicación de como hacer ecuaciones. Estos pasos son muy sencillos y sirven para hacer ecuaciones simples. Para todos aquellos que no entiendan cómo hacer ecuaciones básicas está muy bien explicado en estos 3 cortos videos.
miércoles, 13 de mayo de 2015
Canción de matemática- One Direction
Presentación
Hola a todos! este es nuestro primer post, nuestros nombres son Guido y Valentín . Nuestro objetivo es publicar cosas interesantes acerca de la matemática y enseñar cosas a lo largo de este año.
Suscribirse a:
Entradas (Atom)
%20(1).elp/numden.png)